Double Angle Tan Formula

Double Angle Tan Formula. These identities are summarized in the first two rows of the following table, which also includes sum and difference identities for the other trigonometric functions. ( 2) tan 2 x = 2 tan.

Summary of trigonometric identities from mathcs.clarku.edu

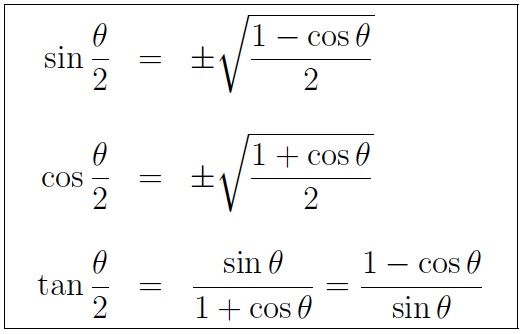
It covers using double angle formulae of sin, cos, and tan to find exact values of trigonometric ratios or verify identities. The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself. The double angle theorem is the result of finding what happens when the sum identities of sine, cosine, and tangent are applied to find the expressions for $\sin (\theta + \theta)$, $\cos (\theta + \theta)$, and $\tan (\theta + \theta)$.

Source: www.slideshare.net

The various formula for multiple angles in trigonometry is discussed in this article. Now, let’s look at the tan 2x trigonometric formulae derivation in detail.

Source: lunlun.com

Trouble applying the tan double angle formula for $5\tan(2\theta)=4\cot(\theta)$ 0. Divide both sides of the equation by 2 next:

Source: www.mymathtables.com

These identities are derived using the angle sum identities. We can substitute the values (2x) (2x) into the sum formulas for \sin sin and \cos.

Source: mathcs.clarku.edu

Are there any probabilistic models for the likelihood of finding a rogue planet closer to us than. Use the double angle formulas for sine and cosine to prove that the double.

Source: evgenii.com

We can substitute the values (2x) (2x) into the sum formulas for \sin sin and \cos. Now, let’s look at the tan 2x trigonometric formulae derivation in detail.

Source: www.youtube.com

On the unit circle, the tangent is negative in the second and. If tan a = 3 / 4, find the values of sin 2a, cos 2a, and tan 2a.

Source: lunlun.com

\(sin(x + y) = sin x cos y + cos x sin y\) 3a, 4a, and so on.

Source: www.nabla.hr

Follow these steps to find the solutions for 2 tan 2 x + 2 = 0 on the interval [0, 2pi): Students can save time while solving problems by learning the multiple angle formulas.

Source: www.meritnation.com

The various formula for multiple angles in trigonometry is discussed in this article. Some important double angle formulas are:

The Multiple Angle Formulas Include The Double And Triple Angle Formulas.

We can substitute the values (2x) (2x) into the sum formulas for \sin sin and \cos. 3a, 4a, and so on. Trouble applying the tan double angle formula for $5\tan(2\theta)=4\cot(\theta)$ 0.

Tan 2 X, Tan 2 Θ, Tan 2 A And Tan 2 Α Are Most Popular Examples For Tan Double Angle Function.

For example, the tangent double angle formula is: Tangent of a double angle. From these formulas, we also have the following identities:

Students Can Save Time While Solving Problems By Learning The Multiple Angle Formulas.

The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself. On the unit circle, the tangent is negative in the second and. With the help of sine and cosine function, tan 2x formula can be derived as follows:

Tips For Remembering The Following Formulas:

We may start by recalling the addition formulae of trigonometry ratios with two angles a and b. There’s a very cool second proof of these formulas, using sawyer’s marvelous idea.also, there’s an easy way to find functions of higher multiples: The common functions employed in the multiple angle formula include sine, tangent, and cosine.

These Identities Are Derived Using The Angle Sum Identities.

In other words, given an angle {eq}\theta {/eq}, the double angle formula is used to calculate {eq. ( 1) tan 2 θ = 2 tan θ 1 − 2 tan 2 θ. The various formula for multiple angles in trigonometry is discussed in this article.